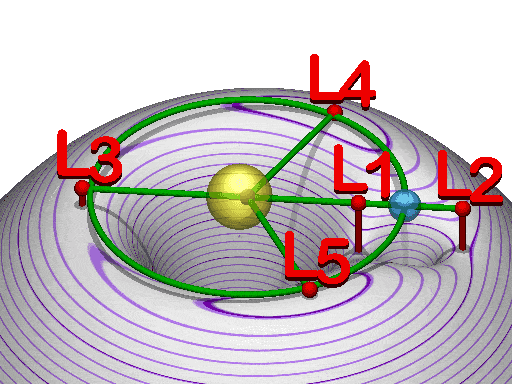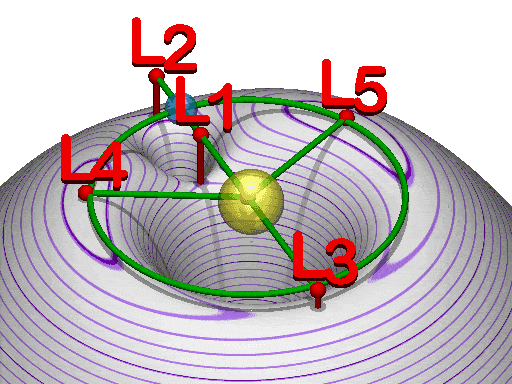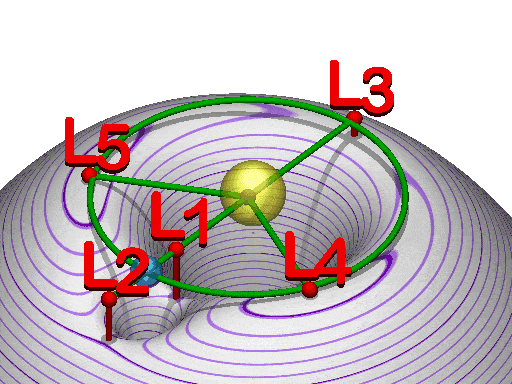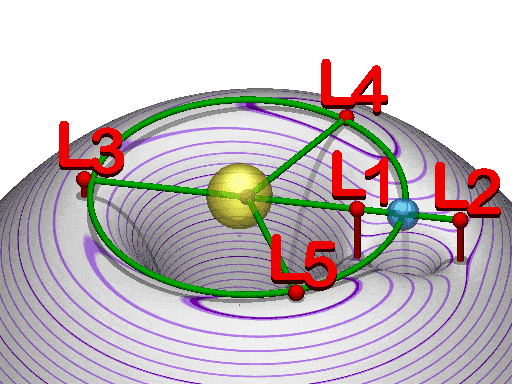
Combined gravitational potential $\phi (x(t),t)$ for Earth--Moon system with Lagrange points.
Motion under gravitation is according to the New View described by the following set of equations in terms of the gravitational potential $\phi (x,t)$ and immaterial free fall trajectories $x(t)$;
Motion under gravitation is according to the New View described by the following set of equations in terms of the gravitational potential $\phi (x,t)$ and immaterial free fall trajectories $x(t)$;
- $\Delta\dot\phi +\nabla\cdot (u\Delta\phi ) = 0$, (mass conservation)
- $u(x(t),t)=\dot x(t)$,
- $\ddot x(t) +\nabla\phi (x(t),t) = 0$, (Newton's 2nd Law)
where the mass density $\rho (x,t)$ does not appear, but is instead tied to $\phi (x,t)$ by the relation $\rho (x,t)=\Delta\phi (x,t)$ by differentiation as instant local action in space. Notice that the immaterial trajectories cover space even where $\Delta\phi (x,t)=0$ expressing absence of matter. The differential equations 1-3 are complemented by initial conditions $\phi (x,0)$ and $x(0)$ and $\dot x(0)$.
To avoid local gravitational collapse from the tendency of gravitational motion to concentrate matter, a pressure force $-\nabla p$ with $p$ a pressure is needed to balance the gravitational force $\rho\nabla\phi$ locally. With such a pressure force present the basic case to consider is a two-body problem as the motion of two bodies 1 and 2 as solid spheres of mass $m_1$ and $m_2$ under gravitation. The corresponding gravitational potential can be expressed as a smoothed version of the potential of the corresponding point masses (in normalized form):
To avoid local gravitational collapse from the tendency of gravitational motion to concentrate matter, a pressure force $-\nabla p$ with $p$ a pressure is needed to balance the gravitational force $\rho\nabla\phi$ locally. With such a pressure force present the basic case to consider is a two-body problem as the motion of two bodies 1 and 2 as solid spheres of mass $m_1$ and $m_2$ under gravitation. The corresponding gravitational potential can be expressed as a smoothed version of the potential of the corresponding point masses (in normalized form):
- $\phi (x,t) =\phi_1(x,t) +\phi_2(x,t)\equiv \frac{m_1}{\vert x - x_1(t)\vert} + \frac{m_2}{\vert x - x_2(t)\vert}$
- $F_{12}(t)=m_1\nabla\phi_2(x_1(t),t) = \frac{m_1m_2}{\vert x_1(t) - x_2(t)\vert^2}e_{12}$,
where $e_{12}$ is a unit vector in the direction $x_2(t) - x_1(t)$, because the the force from $\phi_1$ will be balanced by a local pressure. Likewise the net gravitational force $F_{21}$ acting on body 2 is given by
- $F_{21}(t)=m_2\nabla\phi_1(x_2(t),t) = \frac{m_1m_2}{\vert x_2(t) - x_1(t)\vert^2}e_{21}= -F_{12}(t)$.
We thus recover Newton's law of gravitation, which is no surprise of course, but the important aspect is that the full gravitational potential $\phi (x,t)$ is the sum of the gravitational potentials $\phi_1(x,t)$ and $\phi_2(x,t)$, both changing with time, and that the self-gravitational force with $\nabla\phi_1$ acting on body 1 is balanced by a local pressure and thus effectively is canceled. This means that the trajectory $x_1(t)$ is determined by Newton's 2nd law with $\phi =\phi_2$.
The whole mystery of motion under gravitation is now expressed in the equation $\Delta\dot\phi +\nabla\cdot (u\Delta\phi ) = 0$, which is no mystery since it expresses mass conservation.
The whole mystery of motion under gravitation is now expressed in the equation $\Delta\dot\phi +\nabla\cdot (u\Delta\phi ) = 0$, which is no mystery since it expresses mass conservation.




Hi Claes,
SvaraRaderaSorry this is a bit off topic, I just came across this paper written in 1930 relating the lapse rate & relativity...
The math is way over my head, but thought it would be of interest to you re the lapse rate alone establishing global temperature:
http://authors.library.caltech.edu/2574/1/TOLpr30a.pdf
i am not sure i am following your line of thought.
SvaraRaderathe "mystery" is still there in the equation:
ρ(x,t)=Δϕ(x,t)
that describe a long range force originating from mass and that you use for deriving your result
You are missing the point which is that the potential is primordial and mass derived from potential by differentiation acting locally in space.
SvaraRaderai am not sure i understand what you mean by primordial.
SvaraRaderais the potential there without mass?
what is the origin of this potential?
Primordial means given from start as in Big Bang or whatever. The Laplacian of the gravitational potential can be viewed as being non-zero as a result of a perturbation of the potential from zero as a form of genesis out of nothing.
SvaraRaderaand that is short of a mystery by exactly how much?
SvaraRaderaThat is up to you.
SvaraRadera